Heute ist der 14.03.2021, der Welt Pi Tag (Pi-Day).
Der Grund für diesen Tag liegt an der englischen Schreibweise des Datums.
Monat / Tag = 03/14 = 3,14 = Pi auf 2 Stellen gerundet.
Das Zeichen Pi selber kann man mit der PowerShell als Character erzeugen: [CHAR]960
[char]960 π
Basierend auf dem Artikel vom Heise Newsticker habe ich das dort beschriebene Script für einen Raspberry Pico in die PowerShell Welt portiert.
Da die Kreiszahl Pi eine irrationale Zahl ist, kann sie nicht als Bruch dargestellt werden und deswegen auch nicht berechnet werden. Man kann sich ihr nur durch verschiedene Methoden annähern.
Die hier genutzte Methode nennt sich die Monte-Carlo Methode. Man nimmt ein Quadrat mit einer Kantenlänge von 1 und malt einen Kreis in das Quadrat. Danach berechnet man zufällige Punkte in dem Quadrat und bestimmt, ob der Punkt im Kreis oder außerhalb vom Kreis ist.
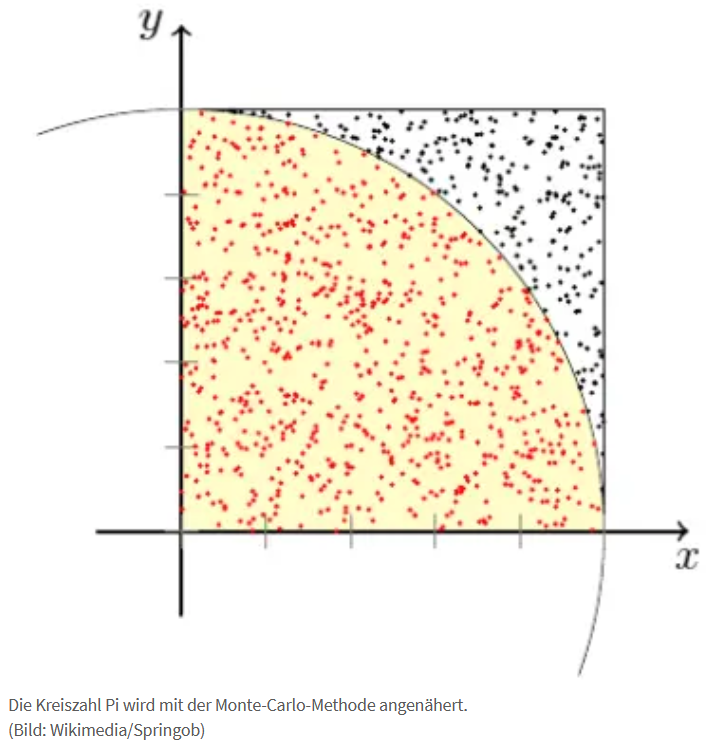
Das Verhältnis von Treffern in der Kreisfläche zu der Gesamtzahl von Durchläufen ergibt 1/4 π.

Zuerst würfeln wir eine x und eine y Koordinate zwischen 0 und 1 aus.
Dafür bietet die PowerShell den Befehl Get-Randon, den ich vor langer Zeit auch hier beschrieben habe. Ich nutze den maximalen Adressraum eines INT32 Wertes.
$x = (Get-Random -Minimum 0 -Maximum ([Int32]::MaxValue)) / ([Int32]::MaxValue)
$y = (Get-Random -Minimum 0 -Maximum ([Int32]::MaxValue)) / ([Int32]::MaxValue)
$x = (Get-Random -Minimum 0 -Maximum ([Int32]::MaxValue)) / ([Int32]::MaxValue) $y = (Get-Random -Minimum 0 -Maximum ([Int32]::MaxValue)) / ([Int32]::MaxValue)
Mit dem Satz des Pythagoras prüfen wir, ob die Koordinate innerhalb des Kreises vom Quadrat mit der Kantenlänge 1 besteht.
Wenn x² + y² kleiner gleich 1 ist, dann ist die Koordinate innerhalb des Kreises
[MATH]::pow($x,2) + [MATH]::pow($y,2)) -le 1
[MATH]::pow($x,2) + [MATH]::pow($y,2)) -le 1
Jetzt muss das ganze noch als Loop laufen mit einer do {} until Schleife.
Die Abbruchbedingung ist eine beliebige Taste: [console]::KeyAvailable
So kann man das Script solange laufen lassen, wie man möchte.
do
{
# der Code
}
until ([console]::KeyAvailable)
Als Ausgabe habe ich Write-Progress gewählt, da die PowerShell nicht immer wieder in die gleiche Zeile schreiben kann.
$pi = ($imkreis*4/$zaehler)
Write-Progress -Activity "Durchlauf $zaehler - $([char]960): $pi"
$pi = ($imkreis*4/$zaehler) Write-Progress -Activity "Durchlauf $zaehler - $([char]960): $pi"
Nach 329104 Durchläufen hat die Annäherung an f Pi immerhin schon auf die ersten 3 Nachkommastellen gestimmt. Ich lasse es aber noch weiterlaufen ...
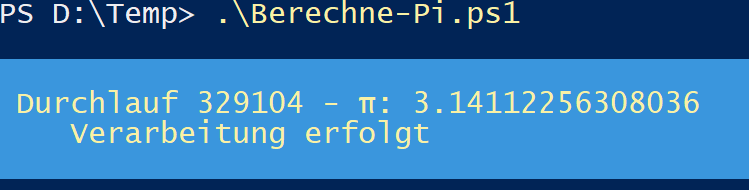
Und hier das ganze Script
# Die Kreiszahl Pi π berechnen
# nach der Monte-Carlo Methode
# BBi / CBC - 20210314
# Man zeichne einen Kreis mit dem Radius 1, umschlossen von einem Quadrat und lässt zufällig Punkte in diesem Quadrat erzeugen
# Das Verhältnis von Treffern in der Kreisfläche zu der Gesamtzahl von Durchlaufen ergibt 1/4 π
# Die Grundidee ist vom Heise Verlag: https://www.heise.de/news/Happy-Pi-Day-Wir-feiern-mit-Kuchen-und-Raspberry-Pi-co-5075899.html
# Funktion zum Testen eines Punktes
function IstImKreis
{
# eine Zahl zwischen 0 und INT32 Max geteilt durch INT32 Max
$x = (Get-Random -Minimum 0 -Maximum ([Int32]::MaxValue)) / ([Int32]::MaxValue)
$y = (Get-Random -Minimum 0 -Maximum ([Int32]::MaxValue)) / ([Int32]::MaxValue)
# Berechnen, ob im Kreis oder nicht
if (([MATH]::pow($x,2) + [MATH]::pow($y,2)) -le 1)
{
# Ist im Kreis
$result = 1
}
else
{
# Ist nicht im Kreis
$result = 0
}
Return $result
}
# Im Kreis Zaehler
$imkreis = 0
# Script laufen lassen bis eine Taste gedrueckt wird
$zaehler = 1
do
{
# PunktInKreis Funktion aufrufen und zaehlen
$imkreis = $imkreis + (IstImkreis)
# Pi abschaetzen
$pi = ($imkreis*4/$zaehler)
Write-Progress -Activity "Durchlauf $zaehler - $([char]960): $pi"
# zaehler erhoehen
$zaehler++
}
until ([console]::KeyAvailable)
# Ergebnis ausgeben
Write-Host "Nach $zaehler Runden ist $([char]960) circa $pi" -foregroundcolor yellow
Viel Spaß beim Nachprogrammieren und Happy Pi Day 🙂


Was denken Sie?